← back to full list
Image compression
Given an image with red, green, and blue values for each pixel, I used various clustering techniques to group pixels of similar color. The image can be compressed, then, by setting each pixel to the mean color value of its cluster. I was less interested in compression itself, though, than in comparing clustering methods.
I give mathematical background and derivations in these PDFs: Expectation Maximization and Spectral Clustering.
Gradients

I wanted to test these clustering algorithms using heavily correlated (in this case, linear) data. Picture the gradients to red and orange as lines in 3-dimensional space. They pass near each other, as red and orange are numerically similar. An algorithm adapted for correlated data, like spectral clustering or EM, manages to keep red and orange separate.

Apples
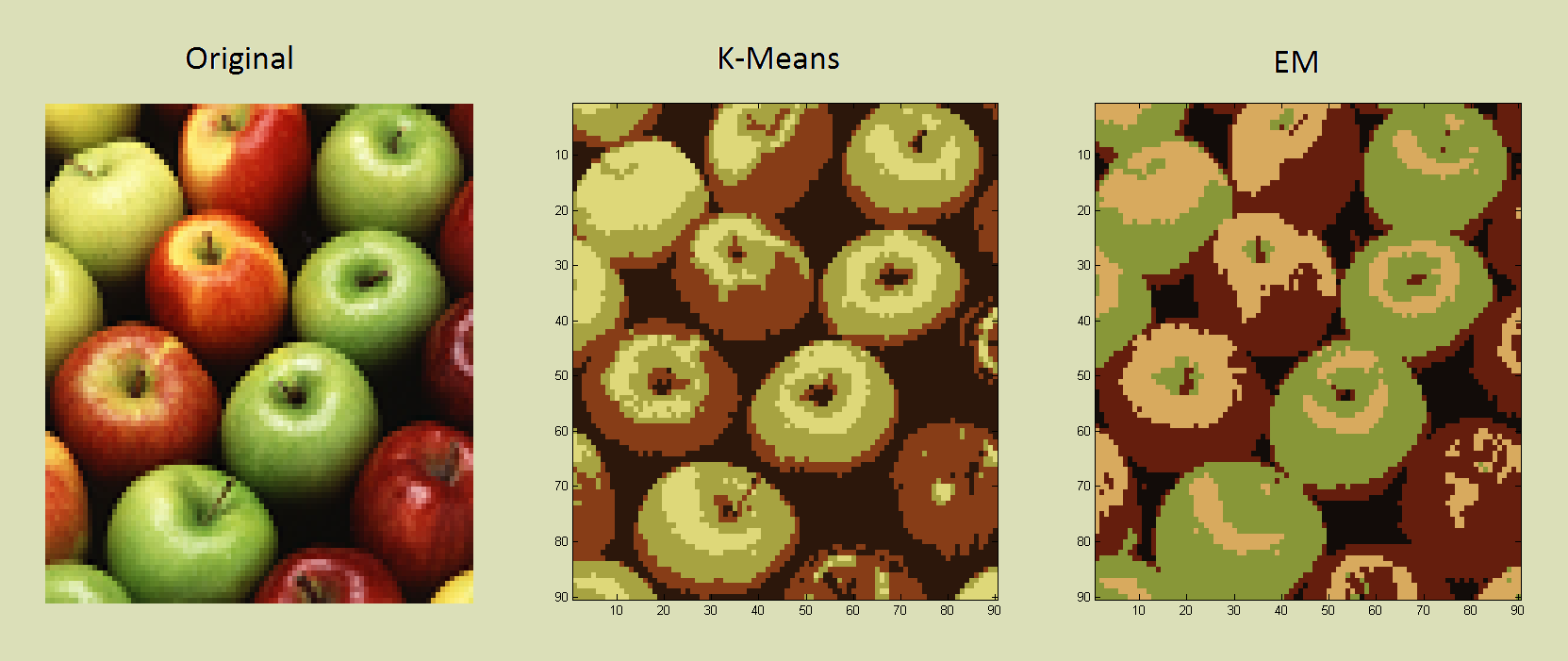
In most image compression, K-means seemed a better choice than EM. In particular, sharp details were clearer (notice the apple stems below). But, as in the gradient example, EM did a better of job at times of keeping similar colors distinct. Note the different apple varieties, using only 4 colors.
Demonstrations
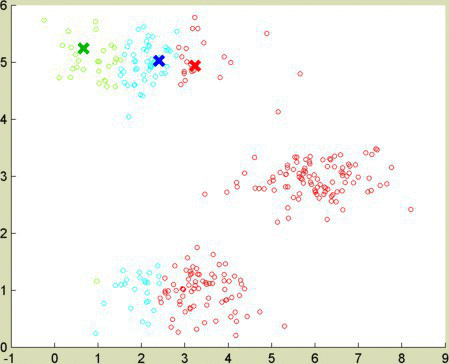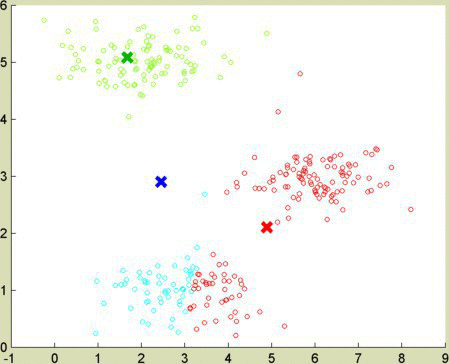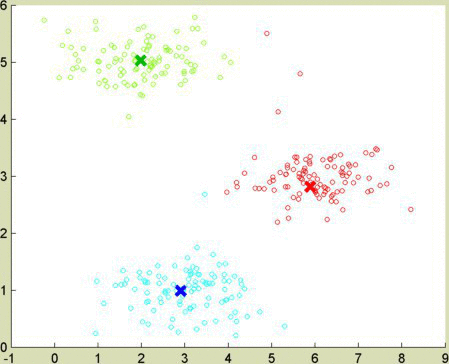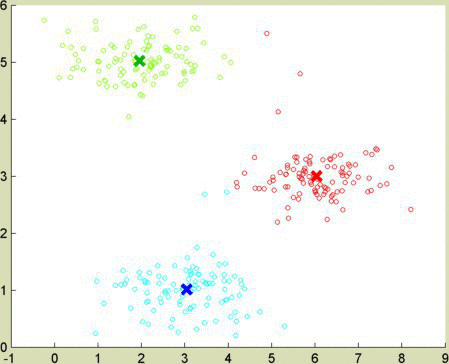
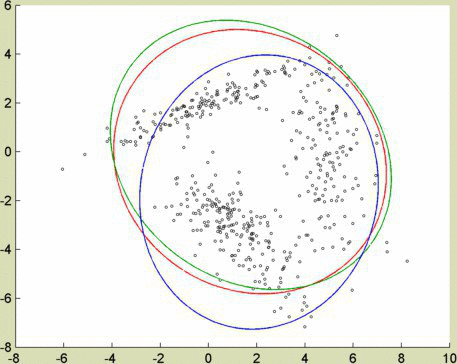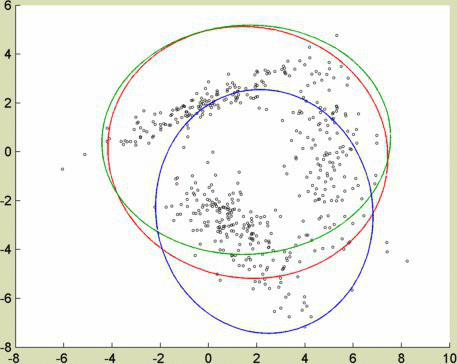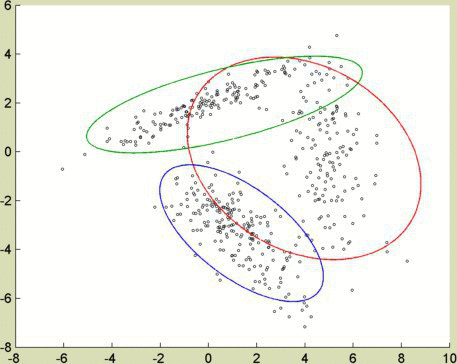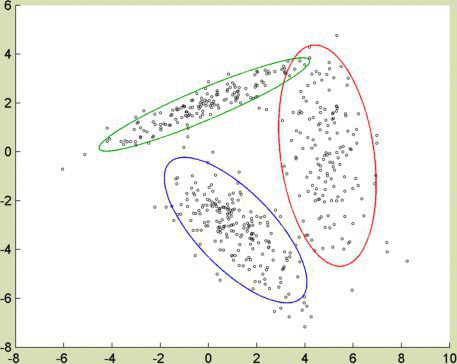
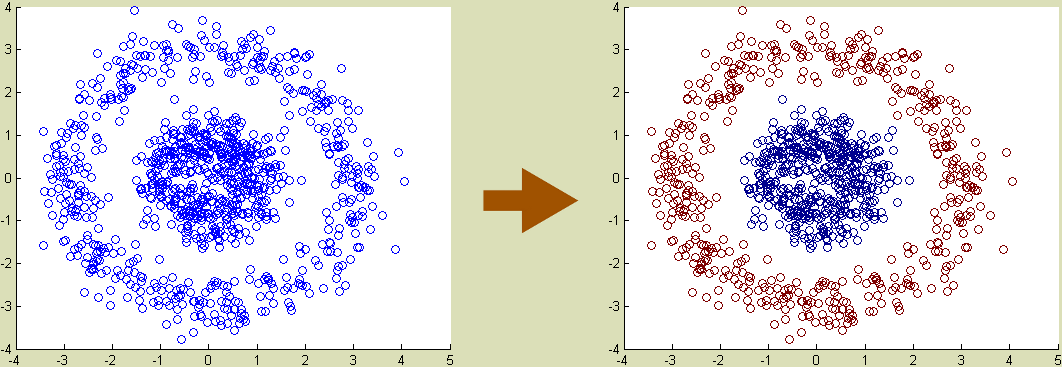
Credits
The data sets for the demos above were provided by Gopal Nataraj, adapted from an EECS 545 course at University of Michigan. I learned the K-means algorithm and the idea to use it to compress images from Andrew Ng’s Machine Learning course at coursera.com. The apple image came from ecigandvaporshop.com.